Regresi Linier Model Laju Pertumbuhan Jenuh
Sunday, November 24, 2013 @ 6:25 AM | 0 Comment Box(s)
1. Pengertian
Regresi Linier Model Laju Pertumbuhan Jenuh Adalah Salah Satu Terapan Dari Regresi Linier. Regresi Linier Model Ini Dapat Digambarkan Dalam Bentuk Grafik Berikut :
Regresi Linier Model Eksponensial Memiliki Bentuk Persamaan - Nya, Yaitu :
Untuk Mendapatkan Persamaan Tersebut Dapat Dicari Dengan Mencari - Nya Lewat Persamaan Berikut :
Di Mana y = 1 /z, a0 = 1 / b0, a1 = b1 / b0, Dan x = 1 / t
2. Langkah - Langkah Pengerjaan
Berikut Contoh Soal Dan Penyelesaian - Nya :
1. Tentukan Persamaan Regresi Linier Model Laju Pertumbuhan Jenuh Dari Data Kinetika Kuman Dalam Tabel Berikut :
Berikut Penyelesaian - Nya :
Menentukan Σx, Σy, Σxy, Σx^2, Σy^2, ybar = Σy / n, xbar = Σx / n, Dan Grafik - Nya
Mencari Nilai - Nilai Dari a1 Dan a0 :
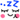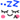Mencari Nilai - Nilai Dari :
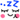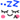Menentukan Model Baik Atau Tidak, Model Baik Jika Sy/x < Sy
Menentukan Persamaan Regresi Model Eksponensial - Nya
Regresi Linier Model Laju Pertumbuhan Jenuh Adalah Salah Satu Terapan Dari Regresi Linier. Regresi Linier Model Ini Dapat Digambarkan Dalam Bentuk Grafik Berikut :
Regresi Linier Model Eksponensial Memiliki Bentuk Persamaan - Nya, Yaitu :
z = ( b0 * t ) / ( b1 + t )
y = a0 + a1x
2. Langkah - Langkah Pengerjaan
Untuk Mendapatkan Persamaan Regresi Linier Model Laju Pertumbuhan Jenuh, Ikuti Langkah -Langkah Berikut :
- Menentukan Σx, Σy, Σxy, Σx^2, Σy^2, ybar = Σy / n, xbar = Σx / n, Dan Grafik - Nya
- Dengan Metode Kuadrat Terkecil, a0 Dan a1 Dapat Dicari Dengan Rumus Berikut :
a1 = n * Σxy - Σx * Σy / n * Σx^2 - Σ( x )^2
a0 = ybar - a1 * xbar
- Menentukan Kesalahan Estimasi Dengan Mencari Nilai - Nilai Berikut :
St = Σy^2 - (( Σy )^2 / n )
Sxy = Σxy - (( Σx * Σy ) / n )
Sr = St - a1 * ( Sxy )
Sy/x = √(Sr / ( n - 2 ))
Sy = √(St / ( n - 1 ))
r = √( 1- (Sr / St ))
- Menentukan Model Baik Atau Tidak, Model Baik Jika Sy/x < Sy
- Menentukan Persamaan Regresi Linier - Nya Dengan Ketentuan Sebagai Berikut :
z = ( b0 * t ) / ( b1 + t )
Berikut Contoh Soal Dan Penyelesaian - Nya :
1. Tentukan Persamaan Regresi Linier Model Laju Pertumbuhan Jenuh Dari Data Kinetika Kuman Dalam Tabel Berikut :
Menentukan Σx, Σy, Σxy, Σx^2, Σy^2, ybar = Σy / n, xbar = Σx / n, Dan Grafik - Nya
Mencari Nilai - Nilai Dari a1 Dan a0 :
a1 = ( n * Σxy - Σx * Σy ) / ( n * Σx^2 - Σ( x )^2 )
a1 = ( 8 * 1.054666 - 0.415635 * 13.99838 ) / ( 8 * 0.039746 - ( 0.415635)^2 )
a1 = 18.036
a1 = ( 8 * 1.054666 - 0.415635 * 13.99838 ) / ( 8 * 0.039746 - ( 0.415635)^2 )
a1 = 18.036
a0 = ybar - a1 * xbar
a0 = 1.749798 - 18.036 *0.051954
a0 = 0.813
Mencari Nilai - Nilai Dari :
St = Σy^2 - (( Σy )^2 / n )
St = 5.927
St = 5.927
Sxy = Σxy - (( Σx * Σy ) / n )
Sxy = 0.327
Sxy = 0.327
Sr = St - a1 * ( Sxy )
Sr =0.022
Sr =0.022
Sy/x = √(Sr / ( n - 2 ))
Sy/x = 0.061
Sy/x = 0.061
Sy = √(St / ( n - 1 ))
Sy = 0.920
Sy = 0.920
r = √( 1- (Sr / St ))
r = 0.998
Menentukan Model Baik Atau Tidak, Model Baik Jika Sy/x < Sy
Sy/x < Sy
0.061 < 0.920
Menentukan Persamaan Regresi Model Eksponensial - Nya
b0 = 1 / a0
b0 = 1.230
b1 = a0 * b0
b1 = 22.184
z = ( b0 * t ) / ( b1 + t )
z = ( 1.230 * t ) / ( 22.184 + t )
Attention !!! :-) :-) :-)
- Put Your Link Or E-mail, And Real Nick Name
- Ask Something, Request Tutorial / Freebies?
- I Will Answer Your Mes On Your Blog Or Your E-Mail Or My Facebook Page(http://www.facebook.com/kormakka?ref=hl)
- And No Harsh Word!
- Keep Smiling :-) :-):-)
Labels: Metode Numerik
